Cathy Humphreys (9th/10th Grade)

Mentor Interview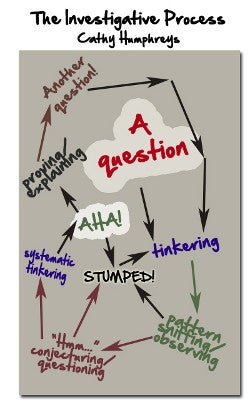

Cathy’s lesson is posed as a “real-world” situation, which motivates a context for her students’ investigations. There are many truly real-world applications of mathematics (e.g., the mathematics of global warming). These applications are especially important for students to experience in order to understand the relevance and importance of mathematics in their lives. During these two days of geometry investigations, Cathy’s students work individually and in small groups to develop convincing arguments (for themselves, for a partner, for a skeptic) about the properties of quadrilaterals. 

Throughout their conversations, her students need to make use of tools strategically. Knowing how to use a tool is very different from knowing when to use it, and students need a lot more practice with
problems that require them to dig deep to find, from all that they know, the tools and ideas that will help them solve a new and unexpected problem.

 

See how Cathy's students demonstrate many mathematical practice standards in one lesson:

1. Make sense of problems and persevere in solving them

Cathy Humphreys leads an extended exploration of a proof of the properties of quadrilaterals, helping students learn to investigate, formulate, conjecture, justify, and ultimately prove mathematical theorems. In this clip, she models how to gather information for the tinkering stage of the investigative process and emphasizes the importance of the process of private individual thinking prior to the group addressing a task. This clip is also indicative of MP6.

See the video in the context of an entire lesson

Continuing into the group section of the task, Humphreys’ students work in teams of four to engage in extended discussion about the properties of kites made by a factory. Their discussion of the properties of quadrilateral shapes proves less complex for some shapes (square, rectangle, rhombus) than for others (non-isosceles trapezoid.) Humphreys circulates around the classroom as the students work, and in her commentary she notes students’ use of imprecise or inaccurate language to defend their thinking. This clip is also indicative of MP3, MP6, and MP7.

See the video in the context of an entire lesson

In the closure of the first day of Humphreys’ students’ exploration, she orients them to the next phase, which will require students to justify and prove their findings about the diagonals of the kites. In this clip, she asks them to “convince yourself, convince a friend, convince a skeptic” with their justifications.

See the video in the context of an entire lesson

On the second day of Humphreys’ exploration of the properties of quadrilaterals, students work through their understandings of congruent triangles, the triangle postulates, parallel lines, transversals, and other geometric properties to apply those to create proofs for the quadrilaterals. Humphreys illustrates how to use selected notation in a proof as students work through the logic and reasoning. In small groups, Cathy Humphreys’ students discuss and debate proof arguments. At selected times, she pulls the class together to share findings, ideas, or sample justifications. After sharing ideas or arguments with the entire class, students then return to working in their small groups.

See the video in the context of an entire lesson

Cathy Humphreys works with her students as they get closer to being able to present their group defenses of the various properties of quadrilaterals. She reminds them about the difference between the properties of a square and a non-square rhombus, and that the groups should keep track of them development of their thinking as they go along. A group of students defines their quadrilateral, then say “Now let’s prove it… we need to not just say that it’s a rhombus, but prove it.” This clip is also indicative of MP3 and MP6.

See the video in the context of an entire lesson

See MP 1 examples from all teachers

3. Construct viable arguments and critique the reasoning of others

Cathy Humphreys leads an extended exploration of a proof of the properties of quadrilaterals, helping students learn to investigate, formulate, conjecture, justify, and ultimately prove mathematical theorems. In these clips, students engage in the first of two block-length explorations of their proofs. The students are in groups of four. Each group has chosen a group member to perform these roles: a team captain, resource manager, recorder, and facilitator. The groups have access to the problem (one page per group), two packets of manipulatives, and other resources that they can retrieve, including a page of definitions of quadrilaterals. In some of the groups, students work individually for a while. In other groups, students work in pairs, and in still others, the entire group of four is collaborating. Humphreys’ commentary notes subtleties in the students’ discourse that either advance or impede the development of their thinking. This clip is also indicative of MP 1, MP 6, and MP7.

See the video in the context of an entire lesson

In the closing of the group work, Humphreys refers her students to the idea of “mathematical friends.” This notion came from Thinking Mathematically by Burton and Mason, a book about mathematical problem solving in which the authors talk about a hierarchy of certainty when trying to write a convincing argument. Convince yourself (the easiest), convince a [mathematical] friend, and finally, convince a skeptic. Developing a skeptical mindset and not jumping to conclusions too quickly is another hallmark of good mathematical thinking. This clip is also indicative of MP6, MP7, and MP 8.

See the video in the context of an entire lesson

On the second day of Humphreys’ exploration of the properties of quadrilaterals, students work through their understandings of congruent triangles, the triangle postulates, parallel lines, transversals, and other geometric properties to apply those to create proofs for the quadrilaterals. The students move between group work and whole class interaction throughout the lesson. In small groups, the students discuss and debate proof arguments. At selected times, the teacher pulls the class together to share findings, ideas, or sample justifications. After sharing ideas or arguments with the entire class, students then return to working in their small groups. This clip is also indicative of MP6.

See the video in the context of an entire lesson

Once each group has worked through the reasoning of the proof, Humphreys checks in with the group and instructs them to begin designing a poster that will display the proof they had created. Groups are instructed to design a poster that contains a drawing of the figure, the conjecture of what is to be proved, a list of the given from the conjecture, and what needs to be proved. The students can use a two column or a flow chart format of the proof. This clip is also indicative of MP1 and MP6.

See the video in the context of an entire lesson

See MP3 examples from all teachers

4. Model with mathematics

Cathy Humphreys leads an extended exploration of a proof of the properties of quadrilaterals, helping students learn to investigate, formulate, conjecture, justify, and ultimately prove mathematical theorems. In this clip, Humphreys introduces the task by posing a problem as a real-life investigation in which a kite manufacturer who “only manufactures quadrilateral kites”, and needs to know the properties of convex quadrilaterals that will always result in a given kite shape, saying “how to do the sticks is the issue.” The students work in groups to give prototype advice to this manufacturer, so that any time an order comes in, the manufacturer will always know “what kind of sticks to put in the kit and how they are to be put together.”

See the video in the context of an entire lesson

See MP4 examples from all teachers

5. Use appropriate tools strategically

Cathy Humphreys leads an extended exploration of a proof of the properties of quadrilaterals, helping students learn to investigate, formulate, conjecture, justify, and ultimately prove mathematical theorems. In this clip, Humphreys circulates around groups of students as they use rulers, protractors, and sheets of paper to make different kinds of quadrilaterals and examine and “guarantee” their properties. A group of students debates whether or not one student’s assertion about the properties of a trapezoid hold in all circumstances, using the kite “sticks” to illustrate their points. This clip is also indicative of MP1.

See the video in the context of an entire lesson

In this clip, Humphreys closes day one of the Properties of Quadrilaterals lesson, and orients students to the second part of the investigation in which they will justify and prove their findings about the diagonals of the kites, saying “convince yourself, convince a friend, convince a skeptic” to describe for students the level of precision necessary to justify their conjectures. The students use definitions, postulates, and theorems to develop a proof about the diagonals of a quadrilateral and how they constrain the type of figure that is formed. Humphreys moves between groups, checking in on the progress students are making in developing their justifications. At the close of the period, she employs the resource manager to make sure all the manipulatives and materials are collected and stored.

See the video in the context of an entire lesson

In this clip, Humphreys articulates the focus for day two of the group investigations of the properties of quadrilaterals: to prove that their conjectures are actually true. She shares examples of how students “kept track” of their own thinking, helping students in their meta-cognitive efforts at understanding how they’re thinking and how to document their understandings. The students mark a figure drawn from the given to help reason through the proof. This clip is also indicative of MP6.

See the video in the context of an entire lesson

In this clip, groups are actively engaged in creating statements about the properties of their quadrilaterals that they can defend. The facilitator asks the resource manager to go get markers, paper, a ruler, and a compass for the group so that they can make their thinking visible. They continue to use the “kite sticks” from Tuesday’s lesson to experiment with different points of intersection. This clip is also indicative of MP6.

See the video in the context of an entire lesson

See MP5 examples from all teachers

6. Attend to precision

Cathy Humphreys leads an extended exploration of a proof of the properties of quadrilaterals, helping students learn to investigate, formulate, conjecture, justify, and ultimately prove mathematical theorems. In this clip, she orients students to the task and explains how they are to communicate their ideas clearly to one anotherduring their group work. This clip is also indicative of MP1.

See the video in the context of an entire lesson

In these clips, Humphreys’ students engage in the first of two block-length explorations of their proofs. The students are in groups of four. Each group has chosen a group member to perform these roles: a team captain, resource manager, recorder, and facilitator. The groups have access to the problem (one page per group), two packets of manipulatives, and other resources that they can retrieve, including a page of definitions of quadrilaterals. In some of the groups, students work individually for a while. In other groups, students work in pairs, and in still others, the entire group of four is collaborating. Humphreys’ commentary notes subtleties in the students’ discourse that either advance or impede the development of their thinking. This clip is also indicative of MP1, MP3, and MP7.

See the video in the context of an entire lesson

In the closing of the group work on the first day, Humphreys refers her students to the idea of “mathematical friends.” This notion came from Thinking Mathematically by Burton and Mason, a book about mathematical problem solving in which the authors talk about a hierarchy of certainty when trying to write a convincing argument. Convince yourself (the easiest), convince a [mathematical] friend, and finally, convince a skeptic. Developing a skeptical mindset and not jumping to conclusions too quickly is another hallmark of good mathematical thinking.

See the video in the context of an entire lesson

In the opening of the second day, Humphreys shares students’ work sheets to illustrate how the students were thinking while investigating the quadrilateral. After sharing work, she has students write to a prompt about how well they keep track of their thinking.. The students then share with the class their individual reflections. The class is still learning how to prove a conjecture. Each group begins to settle on the quadrilateral they will formally prove. The students use their prior knowledge of parallel lines and congruent triangles to approach the proofs of the quadrilaterals. This clip is also indicative of MP5.

See the video in the context of an entire lesson

Continuing their explorations of the properties of quadrilaterals, Humphreys’ students work through their understandings of congruent triangles, the triangle postulates, parallel lines, transversals, and other geometric properties to apply those to create proofs for the quadrilaterals.The students move between group work and whole class interaction throughout the lesson. In small groups, the students discuss and debate proof arguments. At selected times, the teacher pulls the class together to share findings, ideas, or sample justifications. After sharing ideas or arguments with the entire class, students then return to working in their small groups. This clip is also indicative of MP3.

See the video in the context of an entire lesson

Humphreys’ student groups begin to design a poster that contains a drawing of the figure, the conjecture of what is to be proved, a list of the given from the conjecture, and what needs to be proved. The students may use a two column or a flow chart format of the proof. In this clip, a group of students works together to develop their proof. One student summarizes, “So. The definition’s here, the picture and conjecture are done.” They turn to creating a poster to represent their thinking.

See the video in the context of an entire lesson

See MP6 examples from all teachers

7. Look for and make use of structure

Cathy Humphreys leads an extended exploration of a proof of the properties of quadrilaterals, helping students learn to investigate, formulate, conjecture, justify, and ultimately prove mathematical theorems. In these clips, students engage in the first of two block-length explorations of their proofs. Humphreys observes, “The square, rectangle, and rhombus appeared to be the most straightforward for the students. Mathematically, if two of the diagonals form right angles, then at least a pair of sides of the quadrilateral will be equal in length. If the diagonals intersect at the midpoint of both diagonals, then the figure formed will be some parallelogram. In order for two diagonals to form a non-isosceles trapezoid, the following relationships must hold true: If AB is one diagonal and DE is the other diagonal, then trapezoid ADBE is formed only if the diagonals intersect at point P, which is not the midpoint, and AP/PB = DP/PE. This relationship was quite difficult for the students to investigate and conclude. The students did not choose to measure the diagonals with rulers, and therefore did not pick up on the proportional aspects of the diagonals in a non-isosceles trapezoid.” This clip is also indicative of MP1, MP3, and MP6.

See the video in the context of an entire lesson

In the closing of the group work on the first day, Humphreys refers her students to the idea of “mathematical friends.” This notion came from Thinking Mathematically by Burton and Mason, a book about mathematical problem solving in which the authors talk about a hierarchy of certainty when trying to write a convincing argument. Convince yourself (the easiest), convince a [mathematical] friend, and finally, convince a skeptic. Developing a skeptical mindset and not jumping to conclusions too quickly is another hallmark of good mathematical thinking. Humphreys asks to meet with the students who are playing the role of “facilitators” in their groups to ensure that the Burton and Mason argumentation structure is followed. This clip is also indicative of MP3, MP6, and MP8.

See the video in the context of an entire lesson

See MP7 examples from all teachers

8. Look for and express regularity in repeated reasoning 

In the closing of the group work on the first day, Humphreys refers her students to the idea of “mathematical friends.” This notion came from Thinking Mathematically by Burton and Mason, a book about mathematical problem solving in which the authors talk about a hierarchy of certainty when trying to write a convincing argument. Convince yourself (the easiest), convince a [mathematical] friend, and finally, convince a skeptic. This framework helps them test the reasonableness of their results. Humphreys asks to meet with the students who are playing the role of “facilitators” in their groups to ensure that the Burton and Mason argumentation structure is followed. This clip is also indicative of MP3, MP6, and MP7.

See the video in the context of an entire lesson

See MP8 examples from all teachers

See how Cathy's students demonstrate social and emotional learning competencies:

Cathy's lesson is highlighted in the Appendix of Describing the Ideal Classroom, a paper on the shift required by the Common Core State Standards for Mathematical Practice with regard to your classroom culture and collaboration with colleagues. Check out the commentary and video clips on the ways in which her students demonstrate social and emotional learning competencies as they engage with the math practices.