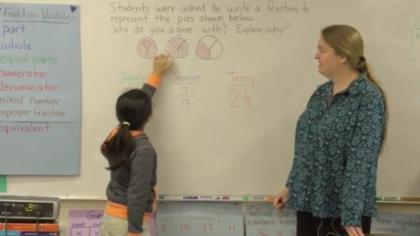Classroom Observations
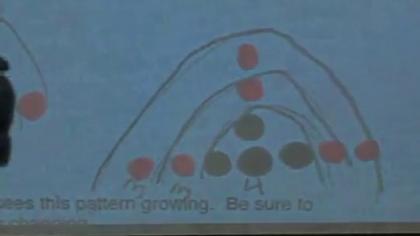
Teachers who are developing students’ capacity to "construct viable arguments and critique the reasoning of others" require their students to engage in active mathematical discourse. This might involve having students explain and discuss their thinking processes aloud, or signaling agreement/disagreement with a hand signal. A middle childhood teacher might post multiple approaches to a problem and ask students to identify plausible rationales for each approach as well as any mistakes made by the mathematician. An early adolescence teacher might post a chart showing a cost-analysis comparison of multiple DVD rental plans and ask his students to formulate and defend a way of showing when each plan becomes most economical. A teacher of adolescents and young adults might actively engage her students in extended conjecture about conditions for proof in the construction of quadrilaterals, testing their assumptions and questioning their approaches. Visit the video excerpts below to view multiple examples of teachers engaging students in formulating, critiquing and defending arguments of mathematical reasoning.
The Standard
Mathematically proficient students understand and use stated assumptions, definitions, and previously established results in constructing arguments. They make conjectures and build a logical progression of statements to explore the truth of their conjectures. They are able to analyze situations by breaking them into cases, and can recognize and use counterexamples. They justify their conclusions, communicate them to others, and respond to the arguments of others. They reason inductively about data, making plausible arguments that take into account the context from which the data arose. Mathematically proficient students are also able to compare the effectiveness of two plausible arguments, distinguish correct logic or reasoning from that which is flawed, and—if there is a flaw in an argument—explain what it is. Elementary students can construct arguments using concrete referents such as objects, drawings, diagrams, and actions. Such arguments can make sense and be correct, even though they are not generalized or made formal until later grades. Later, students learn to determine domains to which an argument applies. Students at all grades can listen or read the arguments of others, decide whether they make sense, and ask useful questions to clarify or improve the arguments.
show more